并不是标准的极大似然法…是魔改的而且效果并比不上人工拟合

因为如果使用标准平均值作为高斯分布的μ，对于中心不在平均点的数据不能很好的拟合

所以改用加权平均

μ = ∑（i=1 to n）（Ai * P(Ai)） 其中P（Ai） 为Ai数值在整个数据集中的出现概率

σ = ∑（i=1 to n)（（Ai – μ）^2 * P(Ai)）* len(A)   其中len(A)为数据种数

直接采用加权方差并不能很好的得到曲线

效果大概：（从1-100 中心点在34-35左右的数据集）

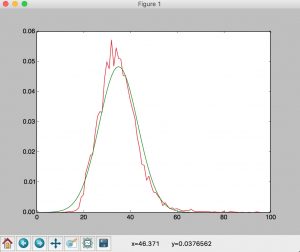
但是貌似对数据缺失没有很好的鲁棒性

接下来应该会去尝试贝叶斯参数估计方法（有点难。。。好难。。。非常难）

这个纯属写着玩= = 没有任何数据依据

import numpy as np
import pylab as pl
from math import sqrt, exp

input_data = []


def read_data(file):
    lines = [line for line in open(file, 'r')]

    for line in lines:
        data = line.split(',')
        input_data.append((int(data[0]), int(data[1])))


def get_data_count():
    data_sum = 0

    for (i, data) in input_data:
        data_sum += data

    return data_sum


def get_avg():
    sum = 0
    gl = get_gl()
    for (a, b) in input_data:
        sum += a * gl[a]

    return sum


def get_gl():
    data_sum = get_data_count()

    result = {u: l / data_sum for (u, l) in input_data}
    return result


def get_jdsrfb():
    N = get_avg()
    gl = get_gl()
    sum = 0;

    for (u, l) in input_data:
        sum += (u - N) * (u - N) * gl[u]

    sum /= len(input_data)
    return N, sum * 100


def get_gaosi(u, N, n):
    PI = 3.14159265358979323
    return 1 / (sqrt(2 * PI) * sqrt(N)) * exp(-(n - u) * (n - u) / (2 * N))


def draw_pic(U, N):
    x_source = []
    y_source = []
    y_target = []
    gl = get_gl()
    for (u, l) in input_data:
        x_source.append(u)
        y_source.append(gl[u])
        y_target.append(get_gaosi(U, N, u))

    pl.plot(x_source, y_source, 'r')
    pl.plot(x_source, y_target, 'g')
    pl.show()


read_data('test.csv')
u, N = get_jdsrfb()
draw_pic(u, N)