应该算是第一个根据自己思路叭出来的Tensorflow 代码

好好地记录一下

首先导入需要的库

import tensorflow as tf
import numpy
import pylab as pl
import Bayesian

pylab为matplotlib的一部分 所以直接使用

pip3 install matpoltlib

就可以安装

Bayesian是上一篇的代码  在这里使用了上一篇计算每个X出现概率的函数

然后是获取属性初始值以及训练数据

x_list = []
y_list = []


def read_data(file):
    lines = [line for line in open(file, 'r')]

    for line in lines:
        data = line.split(',')
        x_list.append(int(data[0]))


Bayesian.read_data('test.csv')
u, N = Bayesian.get_jdsrfb()
gl = Bayesian.get_gl()

read_data('test.csv')
PI = 3.14159265358979323

设置训练参数

# 参数设置
learning_rate = 1
training_epochs = 2000
display_step = 100

导入训练数据，即真实数据

# 训练数据
train_x = numpy.asarray(x_list)
train_y = numpy.asarray([gl[u] for u in x_list])
n_simple = train_x.shape[0]

目的是估计数据集的高斯分布参数

输入数据是[Xi,P(Xi)]

因此定义输入输出 X，P(X) ：

X = tf.placeholder('float')
Y = tf.placeholder('float')

需要估算的参数有两个：

u = tf.Variable(u, name="miu")
N = tf.Variable(N, name="Sigma")

通过参数计算P(X) 即高斯分布的概率密度函数

x = tf.div(1.0, tf.mul(tf.sqrt(2 * PI), tf.sqrt(N)))
y = tf.exp(tf.sub(0.0, tf.div(tf.pow(tf.sub(X, u), 2.0), tf.mul(2.0, N))))

activation = tf.mul(x, y)

Cost函数定义为 “所有X上P(X)预测值和真实值的绝对值的总和”

使用梯度下降算法来使cost最小，即更接近真实值

cost = tf.reduce_sum(tf.abs(Y - activation))
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)

初始化变量

# 初始化变量
init = tf.initialize_all_variables()

根据设定的迭代次数进行计算

每 display_step 次迭代输出当前信息

with tf.Session() as sess:
    sess.run(init)

    # 适配所有变量
    for epoch in range(training_epochs):
        # 未验证上下两种方式哪种更好
        for i in range(training_epochs):
            sess.run(optimizer, feed_dict={X: train_x, Y: train_y})
        # for (x, y) in zip(train_x, train_y):
        #     sess.run(optimizer, feed_dict={X: x, Y: y})

        if epoch % display_step == 0:
            print("Epoch " + str(epoch) + ":  cost=" + str(sess.run(cost, feed_dict={X: train_x, Y: train_y})))
            print("u = " + str(sess.run(u)) + "   N = " + str(sess.run(N)))

    print('Calc Finished!!!')
    print("cost=" + str(sess.run(cost, feed_dict={X: train_x, Y: train_y})))
    print("u = " + str(sess.run(u)) + "   N = " + str(sess.run(N)))

最终可以根据得到的U和N 画图 结果如下

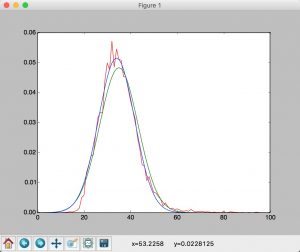
绿色线为极大似然估计结果，蓝色线为经过上述代码迭代后的估计

可见准确度更高