1、Normal Equation 标准矩阵

该方法一次计算即可得出结果。但是也可以多次处理。每次计算取样本数 = 样本特征数 + 1

公式为：

其中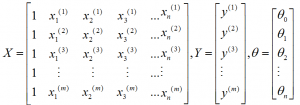

X为训练样本。可见在训练前在每个样本属性前+1

Y为目标结果

Thata即得出的参数矩阵

代码：

    def normal_equation(self):
        data = []
        indexs = []
        while len(indexs) is not self.h_num + 1:
            tmp = random.randint(0, len(self.x_arr) - 1)
            if tmp not in indexs:
                indexs.append(tmp)

        y_data = []
        for index in indexs:
            tmp = copy.deepcopy(self.x_arr[index])
            tmp.insert(0, 1)
            if tmp not in data:
                data.append(tmp)
            y_data.append([self.y_arr[index]])

        data = np.mat(data)
        thata = (data * data.T).I * data.T * np.mat(y_data)
        return thata

上面那个方法中会随机从训练数据中取对应数量的样本加入矩阵

2、局部加权线性回归

该方法在普通的线性回归基础上加上了一个权值wi，使得距离测试点X距离远的数据集对该点参数影响更小。

新的cost公式：

其中w为权值，公式：

这里直接使用Numpy来进行计算：

    def l_r_2(self, test_point, x, y, t=0.1):
        X = np.mat(x)
        Y = np.mat(y)
        m = np.shape(x)[0]
        weights = np.mat(np.eye((m)))
        for j in range(m):
            d = test_point - x[j, :]
            weights[j, j] = np.exp(d * d.T / (-2.0 * t ** 2))
            if np.linalg.det(X.T * weights * X) == 0.0:
                print('矩阵奇异 不能求解')
                return None
        ws = (X.T * weights * X).I * (X.T * (weights * Y))
        return ws

该函数仅求出一个数据点的回归系数

3、岭回归

偷一个图：

代码如下：

def ridgeRegres(xMat, yMat, lam=0.2):  
    xTx = xMat.T*xMat  
    denom = xTx + eye(shape(xMat)[1])*lam  
    if linalg.det(denom) == 0.0:  
        print "This matrix is singular, cannot do inverse"  
    ws = denom.I*(xMat.T*yMat)  
    return ws