牛顿方法中,\\theta的调整方程为:
\(\theta \;=\; \theta + {f(\theta) \over f'(\theta)}\)
其中\({f(\theta) \over f'(\theta)}\)的意义为 函数在x点的切线与x轴的交点x值与x的差值
这样每一次迭代就可以让x值更接近于使\(f(\theta) \;=\; 0\)时的x值。
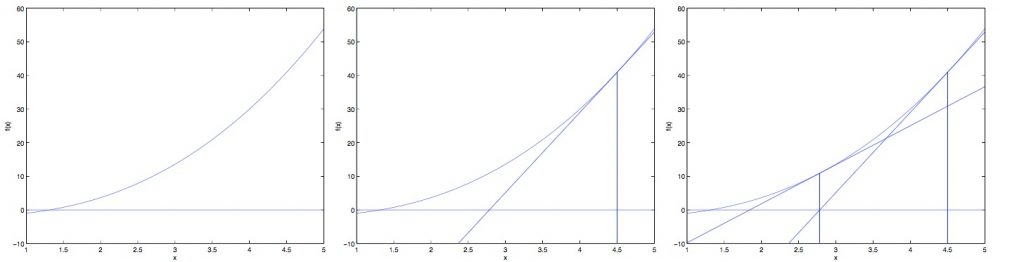
可见在迭代过程中,每一个step的大小都不一样,是越来越小得这跟梯度下降法有很大不同。
那么我们如何使用该方法来找到一个似然函数的最大值?
似然函数的最大值在空间上可以认为在此处梯度为0,即\(\mathscr L'(\theta_0) \;=\; 0\).
则,将该式代入牛顿方法的公式(因为是最大化所以将 + 改为 – ),可以得到:
\(\theta \;=\; \theta – {\mathscr L'(\theta_0) \over \mathscr L”(\theta_0)}\)
在解决逻辑回归问题的过程中,\(\theta\)往往是一个向量,所以我们要考虑将牛顿方法推广至多维的情况,这种推广方法又称为牛顿-拉夫森方法。
\(\theta \;=\; \theta + H^{-1}\nabla_\theta \mathscr L(\theta)\)
其中H被称为海瑟(黑塞)矩阵:
\( H \;=\; \begin{bmatrix} {\partial^2 \mathscr L(\theta) \over \partial\theta_1\partial\theta_1} & \cdots & {\partial^2 \mathscr L(\theta) \over \partial\theta_1\partial\theta_n} \\ \vdots & \ddots & \vdots \\ {\partial^2 \mathscr L(\theta) \over \partial\theta_n\partial\theta_1} & \cdots & {\partial^2 \mathscr L(\theta) \over \partial\theta_n\partial\theta_n} \\ \end{bmatrix} \)
当牛顿方法用来最大化例如逻辑回归的似然函数时,他也被称为fisher scoring
